Boruvka’s Algorithm in Python

   August 19, 2022
Boruvka’s Algorithm in Python

Introduction

In this blog post, we will learn how to code Boruvka’s Algorithm in Python. Algorithms are at the heart of computer science. They are expressed as a finite sequence of operations with well-defined input and output. Boruvka’s approach works by starting with nodes from the input network and growing that forest by adding minimal-weight edges from between its linked components until it becomes a minimum spanning tree of the input graph. Boruvka’s technique has the benefit of not requiring sophisticated data structures to achieve the time complexity constraint. In addition, we are implementing Boruvka’s Algorithm in the Python programming language.

What is Minimum Spanning Tree (MST)?

Assume that T is the spanning tree of the graph G=(V, E), which is a connected, undirected, weighted graph. By calculating the total of the weights of the edges in the spanning tree T, we may give it a weight. A spanning tree that has a weight that is less than or equal to every other spanning tree is referred to as a minimum spanning tree (MST). In general, MST is not unique. If each edge has a different weight, there is only one MST. There are several real-world uses for minimum spanning trees, including network design, tax-anomie, cluster analysis, and more. We would like to provide three traditional polynomial-time techniques for locating MST.

Weighted graph and it's minimum spanning tree
Weighted graph and it’s minimum spanning tree

What is Boruvka’s Approach?

Boruvka’s approach works for a linked network with distinct edge weights, implying a unique MST. The cheapest edge from one node to another in the graph is determined first, without consideration for previously inserted edges. The process of merging these groupings continues until MST is completed. A disjoint-set data structure is used to track MST components. The algorithm is executed in O(Elog V) time. Boruvka’s approach is also applicable to unconnected graphs in our implementation. In that situation, a forest of trees with the shortest possible spread is formed. Furthermore, because our edge comparison uses nodes when weights are identical, repeated edge weights are permitted.

 Boruvka’s  Algorithm:

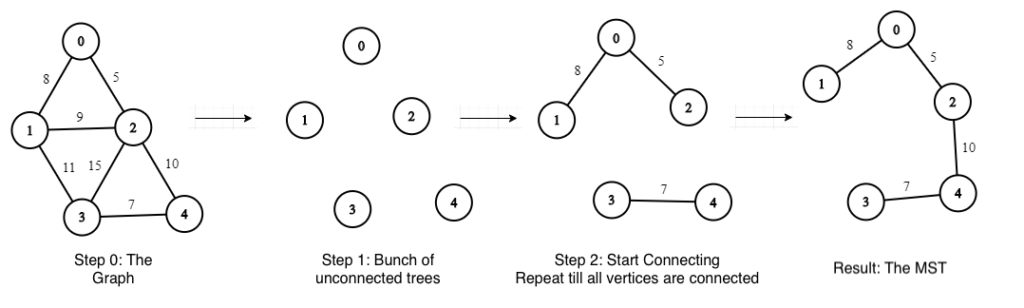
Step 1: Create a graph.
Step 2: Start with a bunch of unconnected trees (number of trees = number of vertices).
Step 3: While there are unconnected trees, for each unconnected tree: find its edge with lesser weight, and add this edge to connect to another tree.

Steps for Boruvka’s  Algorithm in Python

Boruvka’s  Algorithm in Python:

class Graph:
    def __init__(self, vertices):
        self.Destination = vertices
        self.edges = []
        self.component = {}

We will create a Graph class, which will be the primary data structure we will use. Let’s begin with the constructor: We passed the number of nodes in the graph as a parameter to this constructor, and we set three fields: The number of graph nodes, The edge list, The index of the component to which a node belongs is stored in the dictionary.

    def add_edge(self, Source, Destination, weight):
        self.edges.append([Source, Destination, weight])

Furthermore, let’s create a helper function that we can use to add an edge to the nodes of a graph: This function will add an edge to our graph in the format [Source, Destination, weight]. We’ll need a method that propagates a new component throughout a given component before we can create a method that unifies two components. Second, we’ll need a technique for determining the component index of a particular node for Boruvka’s Algorithm in Python.

    def find_component(self, Source):
        if self.component[Source] == Source:
            return Source
        return self.find_component(self.component[Source])

    def set_component(self, Source):
        if self.component[Source] == Source:
            return
        else:
            for k in self.component.keys():
                self.component[k] = self.find_component(k)

In this method, we will consider the dictionary as if it were a tree. We inquire if we have discovered the root of our component since only root components will always point to themselves in the component dictionary. If we haven’t discovered the root node, we seek the current node’s parent recursively.

    def union(self, component_size, Source, Destination):
        if component_size[Source] <= component_size[Destination]:
            self.component[Source] = Destination
            component_size[Destination] += component_size[Source]
            self.set_component(Source)

        elif component_size[Source] >= component_size[Destination]:
            self.component[Destination] = self.find_component(Source)
            component_size[Source] += component_size[Destination]
            self.set_component(Destination)

        print(self.component)

We discover the roots of components for two nodes using this method (which are their component indexes at the same time). Then we compare the sizes of the components and attach the smaller one to the larger one. Then, because they are now one component, we simply add the size of the smaller one to the size of the larger one. Finally, if the components are the same size, we simply join them together any way we like – in this case, by adding the second one to the first. We can now dig into Boruvka’s algorithm now that we’ve developed all of the utility functions we require:

    def boruvka(self):
        component_size = []
        mst_weight = 0

        minimum_weight_edge = [-1] * self.Destination

        for node in range(self.Destination):
            self.component.update({node: node})
            component_size.append(1)

        num_of_components = self.Destination

        print("---------Forming MST------------")
        while num_of_components > 1:
            for i in range(len(self.edges)):

                Source = self.edges[i][0]
                Destination = self.edges[i][1]
                w = self.edges[i][2]

                Source_component = self.component[Source]
                Destination_component = self.component[Destination]

                if Source_component != Destination_component:
                    if minimum_weight_edge[Source_component] == -1 or \
                            minimum_weight_edge[Source_component][2] > w:
                        minimum_weight_edge[Source_component] = [Source, Destination, w]
                    if minimum_weight_edge[Destination_component] == -1 or \
                            minimum_weight_edge[Destination_component][2] > w:
                        minimum_weight_edge[Destination_component] = [Source, Destination, w]

            for node in range(self.Destination):
                if minimum_weight_edge[node] != -1:
                    Source = minimum_weight_edge[node][0]
                    Destination = minimum_weight_edge[node][1]
                    w = minimum_weight_edge[node][2]

                    Source_component = self.component[Source]
                    Destination_component = self.component[Destination]

                    if Source_component != Destination_component:
                        mst_weight += w
                        self.union(component_size, Source_component, Destination_component)
                        print("edge_Added [" + str(Source) + " - "
                              + str(Destination) + "]\n"
                              + "weight_Added: " + str(w) + "\n")
                        num_of_components -= 1

            minimum_weight_edge = [-1] * self.Destination
        print("-------------CopyAssignment.com---------------------")

The first step in this technique was to create a list of components and nodes for Boruvka’s Algorithm in Python. Following that, we constructed an A list that keeps their size initialized to 1, as well as a list of the minimum weight edges, which is initially -1 because we don’t know what the minimum weight edges are.

Secondly, for each edge in the graph, we find the root of the components on both sides of that edge. Then, using a pair of if clauses, we hunt for the minimal weight edge that links these two components:

  1. We will assign the value of the edge we are now monitoring to the least weight edge of Source if it exists (is -1), or if it is larger than it.
  2. We will allocate the value of the edge we are now monitoring to the minimal weight edge of Destination if it exists (is -1), or if it is larger than it.

After we’ve determined the cheapest edges for each component, we add them to the minimal spanning tree and reduce the number of components correspondingly.

Finally, we reset the list of minimal weight edges to -1 so that we may repeat the process. We keep iterating as long as there is more than one component in the list of components.

Let us take the graph as the input to our developed algorithm:

Complete Code of Boruvka’s  Algorithm in Python for minimum spanning trees

class Graph:
    def __init__(self, vertices):
        self.Destination = vertices
        self.edges = []
        self.component = {}
    def add_edge(self, Source, Destination, weight):
        self.edges.append([Source, Destination, weight])
    def find_component(self, Source):
        if self.component[Source] == Source:
            return Source
        return self.find_component(self.component[Source])

    def set_component(self, Source):
        if self.component[Source] == Source:
            return
        else:
            for k in self.component.keys():
                self.component[k] = self.find_component(k)

    def union(self, component_size, Source, Destination):
        if component_size[Source] <= component_size[Destination]:
            self.component[Source] = Destination
            component_size[Destination] += component_size[Source]
            self.set_component(Source)

        elif component_size[Source] >= component_size[Destination]:
            self.component[Destination] = self.find_component(Source)
            component_size[Source] += component_size[Destination]
            self.set_component(Destination)

        print(self.component)

    def boruvka(self):
        component_size = []
        mst_weight = 0

        minimum_weight_edge = [-1] * self.Destination

        for node in range(self.Destination):
            self.component.update({node: node})
            component_size.append(1)

        num_of_components = self.Destination

        print("---------Forming MST------------")
        while num_of_components > 1:
            for i in range(len(self.edges)):

                Source = self.edges[i][0]
                Destination = self.edges[i][1]
                w = self.edges[i][2]

                Source_component = self.component[Source]
                Destination_component = self.component[Destination]

                if Source_component != Destination_component:
                    if minimum_weight_edge[Source_component] == -1 or \
                            minimum_weight_edge[Source_component][2] > w:
                        minimum_weight_edge[Source_component] = [Source, Destination, w]
                    if minimum_weight_edge[Destination_component] == -1 or \
                            minimum_weight_edge[Destination_component][2] > w:
                        minimum_weight_edge[Destination_component] = [Source, Destination, w]

            for node in range(self.Destination):
                if minimum_weight_edge[node] != -1:
                    Source = minimum_weight_edge[node][0]
                    Destination = minimum_weight_edge[node][1]
                    w = minimum_weight_edge[node][2]

                    Source_component = self.component[Source]
                    Destination_component = self.component[Destination]

                    if Source_component != Destination_component:
                        mst_weight += w
                        self.union(component_size, Source_component, Destination_component)
                        print("edge_Added [" + str(Source) + " - "
                              + str(Destination) + "]\n"
                              + "weight_Added: " + str(w) + "\n")
                        num_of_components -= 1

            minimum_weight_edge = [-1] * self.Destination
        print("-------------CopyAssignment.com---------------------")
        print("The minimum spanning tree is overall weighed is: " + str(mst_weight))

g = Graph(9)
g.add_edge(0, 1, 4)
g.add_edge(0, 6, 7)
g.add_edge(1, 6, 11)
g.add_edge(1, 7, 20)
g.add_edge(1, 2, 9)
g.add_edge(2, 3, 6)
g.add_edge(2, 4, 2)
g.add_edge(3, 4, 10)
g.add_edge(3, 5, 5)
g.add_edge(4, 5, 15)
g.add_edge(4, 7, 1)
g.add_edge(4, 8, 5)
g.add_edge(5, 8, 12)
g.add_edge(6, 7, 1)
g.add_edge(7, 8, 3)
g.boruvka()

The output of Boruvka’s  Algorithm:

Output for Boruvka’s Algorithm in Python

Conclusion

In this article, we demonstrated a Python version of Boruvka’s algorithms. The algorithms are represented by classes, and graph objects are handled using the suggested graph interface. In some aspects, the provided implementation is unique. The source code is comprehensible in the same way that pseudocode from textbooks or scientific publications is. On the other hand, the code can be run with the efficiency specified by the associated theory. Python’s class system adds classes with little additional syntax, and it is simple to design desired data structures (e.g., an edge, a graph, a union-find data structure) or to use objects from standard modules (e.g., queues, stacks).

Thank you for visiting our website.

Also Read:

Share:

Author: Ayush Purawr