Search A 2D Matrix: Leetcode 74

Hello everyone, in this article we are going to discuss a very famous DSA problem Search a 2D matrix(https://leetcode.com/problems/search-a-2d-matrix/). It is a leetcode medium–level problem. We will discuss the problem statement, solution approach, and different methods to solve the problem.

Problem Statement

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

Integers in each row are sorted from left to right
The first integer of each row is greater than the last integer of the previous row

Example 1

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Problem Explanation

This problem is very simple and straightforward. We have to search for an element in the 2D matrix, if the element is present in the matrix, we will return true else we will return false.

Solutions to Search a 2D matrix: leetcode 74

1. Brute Force solution approach to the problem

For brute force we can traverse the matrix with the help of two for loops and compare every element with the element given, if any element matches the given element, we return true else we return false.

This approach requires O(N^2) time complexity and O(1) space complexity.

2. O(m*n) Approach

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    int m = matrix.size();
    int n = matrix[0].size();
    for(int i = 0;i<m;i++) 
        {             
            for(int j = 0;j<n; j++)
                if(matrix[i][j] == target)
                    return true; 
        }
    return false; 
}

3. O(log(m*n)) Approach

We can reduce the time complexity of the question to O(log(m*n)) by using binary search on a 2D matrix.

Here we will see how we can apply binary search on 2D matrix, if we look at our problem carefully, our matrix is sorted, which gives a hint that binary search can be applied.

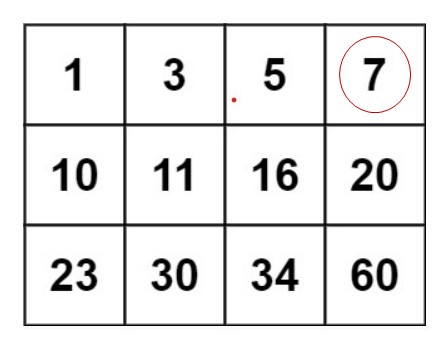
Let us say, the matrix in the image above is given as an example and we have to search 3.

We will start comparing from the top right element in our case 7, we compare this element to 3, 3 < 7 we shift to the left in the same row.

O(log(m*n)) Approach leetcode 74 Search a 2D matrix

Now we are on 5, again 3 < 5, and we shift to more left.

Now if we compare, 3==3 so we will return true.

C++ code for O(log(m*n)) Approach

bool searchMatrix(vector<vector<int>>& matrix, int target) {
    
    int m = matrix.size();
    int n = matrix[0].size();
    
    //initializing I and j to top right element
    int i = 0, j = n - 1;
    
    //controlling the loop
    while(i >= 0 && i < m && j >= 0 && j < n)
    {
         //checking conditions
        if(matrix[i][j] < target)
            i++;
        else if(matrix[i][j] > target)
            j--;
        //returning true if element found
        else if(matrix[i][j] == target)
            return true;
    }
    
    //returning false if element not found.
    return false;
}

Best 100+ Python Projects with source code

Also Read: