Given some numbers, we need to find whether they are smart numbers or not. If they are smart we should print “YES” otherwise print “NO”.
A smart number is defined as a number that has an odd number of factors.
We have to perform debugging of the code. We can only modify one line of code and can not add or delete any line.
Given Code
import math
def is_smart_number(num):
val = int(math.sqrt(num))
if num / val == 1:
return True
return False
for _ in range(int(input())):
num = int(input())
ans = is_smart_number(num)
if ans:
print("YES")
else:
print("NO")We can only modify one line in this code.
Approach for Smart Number Hackerrank Solution
The different factors of a number form pairs among each other. If x is a factor of a number n, we know that n/x will also be a factor of that number. For example, 2 is a factor of 10, then 10/2, 5 is also a factor of 10.
This is the approach that we use to find factors of a number in O(sqrt(n)) time complexity. We just loop through all numbers till sqrt(n). If it is a factor we add that number and also n divided by that number to the list of factors. So we always get a pair of factors.
The only time we can have an odd number of factors is if x = n/x. Thus the factor is its own pair. This equation can be simplified as n = x^2 Or x = sqrt(n).
So, if an integer square root of n exists that is if n is a perfect square, we get an odd number of factors, making it a special number.
Thus, we can update the condition to check for this.
if num / val == 1:
becomes
if num / val == val:
Smart Number Hackerrank Solution
import math
def is_smart_number(num):
val = int(math.sqrt(num))
if num / val == val:
return True
return False
for _ in range(int(input())):
num = int(input())
ans = is_smart_number(num)
if ans:
print("YES")
else:
print("NO")Output:
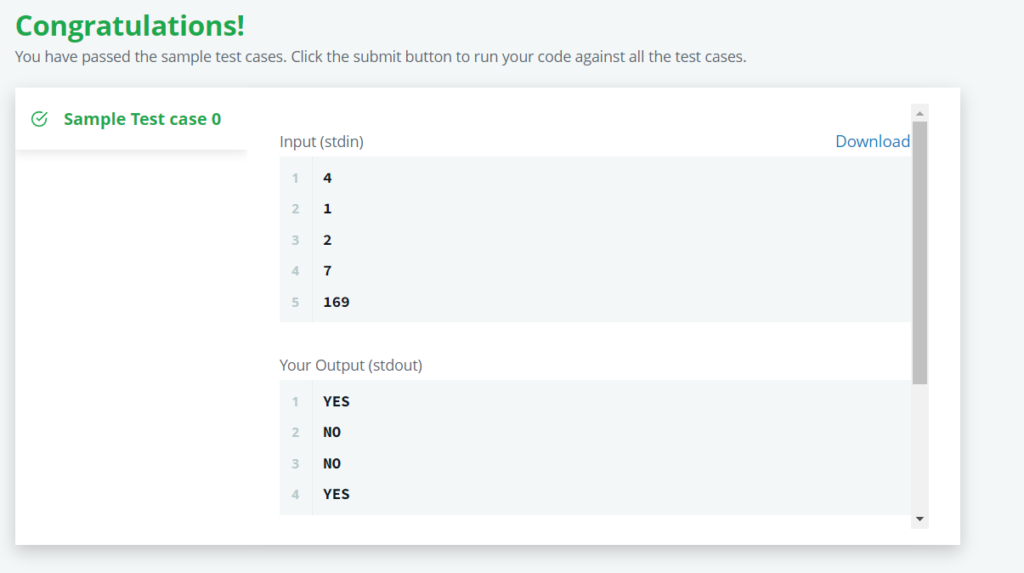
Also Read:
- Download 1000+ Projects, All B.Tech & Programming Notes, Job, Resume & Interview Guide, and More – Get Your Ultimate Programming Bundle!
- HackerRank Day 8 Solution in Python: Dictionaries and Maps
- HackerRank Day 7 Solution in Python: Arrays
- HackerRank Day 6 Solution in Python: Let’s review
- HackerRank Day 5 Solution in Python: Loops
- HackerRank Day 4 Solution in Python: Class vs Instance
- HackerRank Day 3 Solution in Python: Intro to Conditional Statements
- HackerRank Day 2 Solution in Python: Operators
- HackerRank Day 1 Solution in Python: Data Types
- HackerRank Day 0 Solution in Python: Hello World
- HackerRank Day 29 Solution in Python: Bitwise AND
- HackerRank Day 28 Solution in Python: RegEx, Patterns, and Intro to databases
- HackerRank Day 27 Solution in Python: Testing
- HackerRank Day 26 Solution in Python: Nested Logic
- HackerRank Day 25 Solution in Python: Running Time and Complexity
- HackerRank Day 24 Solution in Python: More Linked Lists
- HackerRank Day 23 Solution in Python: BST Level Order Traversal
- HackerRank Day 22 Solution in Python: Binary Search Trees
- Find Peak Element LeetCode 162
- HackerRank Day 20 Solution in Python: Sorting
- HackerRank Day 19 Solution in Python: Interfaces
- HackerRank Day 18 Solution in Python: Queues and Stacks
- HackerRank Day 17 Solution in Python: More Exceptions
- HackerRank Day 16 Solution: Exceptions – String to Integer
- Explained: Allocate minimum number of pages
- HackerRank Day 15 Solution in Python: Linked List
- Search a 2D matrix: leetcode 74
- Maximum Subarray Sum: Kadane’s Algorithm
- HackerRank Day 13 Solution in Python: Abstract Classes
- HackerRank Day 14 Solution in Python: Scope

