Definition
Sudoku is a simple number game that involves a grid of nine-by-nine boxes. Numbers from one to nine fill the boxes. No number can occur twice in each row and each column. So, today we will try the Sudoku solver Python program. Click here to get complete code.
Bigger boxes are formed three by three smaller boxes. The same rule applies that no number can be repeated within the larger boxes.
You can solve a sudoku puzzle in several ways but we are going to use python to make a simple program to solve it. This will take a few minutes and to make it so simple, we are not going to use any modules or anything complex for that matter. However, coding such a program provides a limitless number of ways to solve it. Let’s make use of two methods that make the program much simpler and run faster. These two important methods we are going to imply are recursion and backtracking.
Recursion
Recursion involves calling a function within a function. You will come to understand this when we need to call the function several times to solve an unknown number.
Backtracking
Backtracking involves inserting a possible number in the nearest empty box and going to the next unsolved box. This will go on until we run into an error and we place a zero in the box. We move to the previously solved box and try the next possible number to solve it.
Loading a board
So let’s get to it. We first need to load a board that we will have to solve:
board=[
[5,3,0,0,7,0,0,0,0],
[6,0,0,1,9,5,0,0,0],
[0,9,8,0,0,0,0,6,0],
[8,0,0,0,6,0,0,0,3],
[4,0,0,8,0,3,0,0,1],
[7,0,0,0,2,0,0,0,6],
[0,6,0,0,0,0,2,8,0],
[0,0,0,4,1,9,0,0,5],
[0,0,0,0,8,0,0,7,9]]When printing out this board, it might look messy. We use a “print_board” to make the board look neater.
#We shorten the board name to bo for easy usage
def print_board(bo):
for i in range(len(bo)):
if i%3 == 0 and i!=0:
print("---------------------")
#This prints a horizontal line between the bigger boxes
for j in range(len(bo[0])):
if j%3 == 0 and j!=0:
print(" | ", end ="")
if j==8:
print(bo[i][j])
else:
print(str(bo[i][j]) + " ",end="")
#This prints a vertical line between the bigger boxesFinding empty slots
To solve the sudoku, we first need to find an empty box. We define a function for this. The function returns the position of the empty box denoted by zero. It returns None if there are no more empty boxes which means that the puzzle has been solved.
def find_empty(bo):
for i in range(len(bo)):
for j in range(len(bo[0])):
if bo[i][j] == 0:
return (i, j)
return NoneOnce we get the position of empty boxes, we need to have a function that will check the possible solutions for each box. This means you have to check if the number has occurred in the same column or same row or within the bigger box. These are three things we need to check.
Validity of a number to be inserted
The function we are going to define here takes three parameters; the board, the number we are checking and the position it is going to be inserted within the board. If the number has occurred within the above three cases, we return a False, and a new value is inserted. If it passes all three cases we return a True and proceed to the next unsolved box.
def valid(bo, num, pos):
#We first check if the number has occurred within the row
for i in range(len(bo[0])):
if bo[pos[0]][i] == num and pos[1]!= i:
return False
#We then check if the number has occurred within the column
for j in range(len(bo)):#checking column
if bo[i][pos[1]] == num and pos[0]!= i:
return False
#We finally check if the number has occurred within the bigger box
box_x = pos[1]//3
box_y = pos[0]//3
for i in range(box_y*3, box_y*3 + 3):
for j in range(box_x*3, box_x*3 + 3):
if bo[i][j] == num and (i,j) != pos:
return False
return TrueSolving the sudoku puzzle
After doing all these, we finally arrive at the final function that is quite important. The solve function takes the board as a parameter. We first find empty slots on the sudoku board. After doing so we need to check if the board has been solved, if so we return True which exits the functions. If not we update the new empty slots. We now try plugging in numbers one to nine to the empty slots if possible. We check if the number can be inserted and if true we plug it in. To move to the next empty slot we recur the same process until there are no more empty slots. Hence the term recursion. We recall the function within itself.
However, we do this to find a possible solution and if we run into a dead end we backtrack. This means that we replace the slot we just filled with a zero and move back to the previously solved slot and try the next possible solution.
def solve(bo):
find = find_empty(bo)
if not find:
#This means that the find function came back null.
#This implies that the sudoku has been solved.
return True
else:
row, col = find
for i in range(1,10):
if valid(bo, i , (row,col)):
#If the number can be plugged in at the empty slot, we insert it.
bo[row][col] = i
#We then recall the function to solve the next empty slot.
if solve(bo):
return True
#When we run into an error, we backtrack.
#We do this by placing a zero to the previously solved slot.
bo[row][col]=0
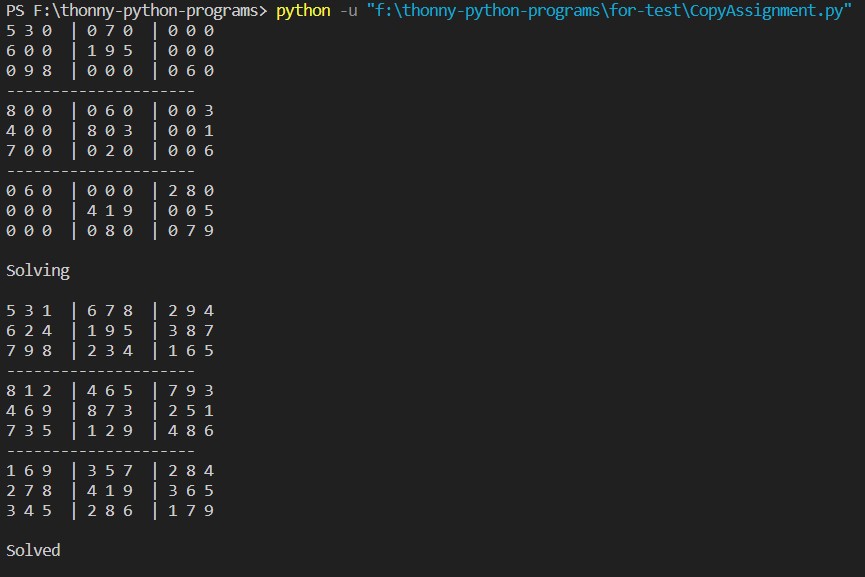
return FalseWe finish off by printing the board before the solution and calling the solve function. We insert a line to differentiate the solved board and the unsolved board. And we print the finished board. We use the custom print function to print out the boards neatly.
print_board(board)
solve(board)
print("Solving")
print_board(board)Let us now see the finished code combining the above functions and board.
board=[
[5,3,0,0,7,0,0,0,0],
[6,0,0,1,9,5,0,0,0],
[0,9,8,0,0,0,0,6,0],
[8,0,0,0,6,0,0,0,3],
[4,0,0,8,0,3,0,0,1],
[7,0,0,0,2,0,0,0,6],
[0,6,0,0,0,0,2,8,0],
[0,0,0,4,1,9,0,0,5],
[0,0,0,0,8,0,0,7,9]]
def print_board(bo):
for i in range(len(bo)):
if i%3 == 0 and i!=0:
print("---------------------")
for j in range(len(bo[0])):
if j%3 == 0 and j!=0:
print(" | ", end ="")
if j==8:
print(bo[i][j])
else:
print(str(bo[i][j]) + " ",end="")
def find_empty(bo):
for i in range(len(bo)):
for j in range(len(bo[0])):
if bo[i][j] == 0:
return (i, j)
return None
def valid(bo, num, pos):
for i in range(len(bo[0])):#checking row
if bo[pos[0]][i] == num and pos[1]!= i:
return False
for j in range(len(bo)):#checking column
if bo[i][pos[1]] == num and pos[0]!= i:
return False
box_x = pos[1]//3
box_y = pos[0]//3
for i in range(box_y*3, box_y*3 + 3):
for j in range(box_x*3, box_x*3 + 3):
if bo[i][j] == num and (i,j) != pos:
return False
return True
def solve(bo):
find = find_empty(bo)
if not find:
return True
else:
row, col = find
for i in range(1,10):
if valid(bo, i , (row,col)):
bo[row][col] = i
if solve(bo):
return True
bo[row][col]=0
return False
print_board(board)
solve(board)
print("Solving")
print_board(board)
print("Solved")Output:
Thanks for reading through my article.
Please comment with your questions or anything wrong you found with this article.
Check the other posts below–
Jarvis and Google Assistant || Voice Assistant Using Python
Get Any Country Date And Time Using Python

