NxNxN Matrix In Python 3

A 3d matrix(NxNxN) can be created in Python using lists or NumPy. Numpy provides us with an easier and more efficient way of creating and handling 3d matrices. We will look at the different operations we can provide on a 3d matrix i.e. NxNxN Matrix in Python 3 using NumPy.

Create an NxNxN Matrix in Python 3

To create a 3d NxNxN with Python 3, one has to manually declare the matrix or create it using nested list comprehensions. While matrix creation with NumPy is very simple. We just need to specify the shape and the data type of the matrix. Below are examples of creating a 3d matrix(NxNxN Matrix in Python 3) with NumPy.

Matrix of zeros with Python

from pprint import pprint

arr = [[[0 for i in range(3)] for j in range(3)] for k in range(3)]
pprint(arr)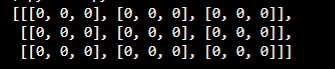

Matrix of zeros with NumPy

import numpy as np
from pprint import pprint

arr = np.zeros((3,3,3), dtype=int)
pprint(arr)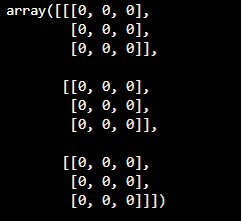

Matrix of ones

import numpy as np
from pprint import pprint

arr = np.ones((2,4,3), dtype=int)
pprint(arr)

Matrix with random values

A 4x4x4 matrix with random values between 0 and 100.

import numpy as np
from pprint import pprint

arr = np.random.randint(0, 100, size=(4, 4, 4))
pprint(arr)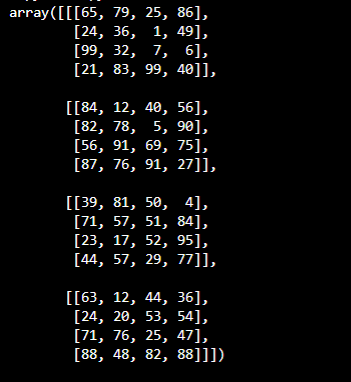

Output- 3D NxNxN Matrix with random values with NumPy in Python 3

Convert python list to NumPy matrix

We can convert python lists to NumPy matrixes just by calling the NumPy array function with our list as the argument.

import numpy as np
from pprint import pprint

arr = [[[1,3,2], [2,3,2]], [[4,2,9], [8,6,0]]]
arr2 = np.array(arr)
pprint(arr2)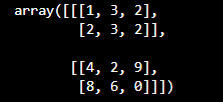

Output - Convert python list to NumPy matrix

Matrix Slicing of 3D NxNxN Matrix in Python

Matrix slicing is taking out a part of the matrix. This is done by giving the start and end coordinates.

import numpy as np
from pprint import pprint

arr = np.random.randint(0, 100, size=(3, 3, 3))
pprint(arr)

sliced = arr[1:3, 1:3, 1:3]
print('\nSliced matrix:\n')
pprint(sliced)

Output- NxNxN Matrix in Python 3: Matrix Slicing

Transpose a 3D NxNxN Matrix in Python with NumPy

Matrix transposition is the interchanging of rows and columns of the matrix. This can be done easily in a single line using NumPy.

import numpy as np
from pprint import pprint

arr = np.random.randint(1, 10, size=(3, 3, 3))
pprint(arr)

trans = np.transpose(arr)
print('\nTransposed matrix:\n')
pprint(trans)

Transpose an NxNxN Matrix in Python with NumPy

Rotation of 3D NxNxN Matrix with NumPy

A matrix can be rotated by 90 degrees or multiples of 90 degrees using the rot90 function. It takes in the matrix, the number of times to rotate the matrix and axes as parameters.

import numpy as np
from pprint import pprint

arr1 = np.random.randint(1, 10, size=(2, 3, 2))
print("Matrix 1:\n")
pprint(arr1)

rot = np.rot90(arr1, 1)
print("\nMatrix Rotation:\n")
pprint(rot)

Rotation of NxNxN 3D matrix with NumPy in Python

Summation of the NxNxN 3D matrix along different axes

Summation along axis 0

Considering a 3X3X3 matrix of random digits. Over here the (i,j)th element of each 3X3 matrix is added with the (i,j)th element of the remaining matrices. We get a 3X3 matrix as output.

import numpy as np
from pprint import pprint

arr = np.random.randint(1, 10, size=(3, 3, 3))
print("Matrix:\n")
pprint(arr)

arr_sum = np.sum(arr, axis=0)
print("\nMatrix sum along axis 0:\n")
pprint(arr_sum)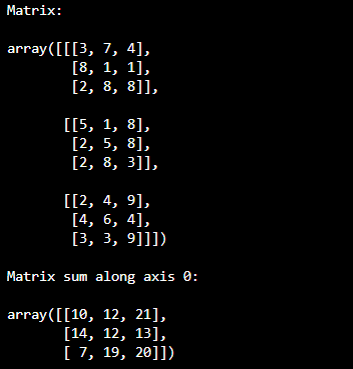

Summation along axis 1

Considering a 3X3X3 matrix of random digits. The elements are added across the columns. We get a 3X3 matrix as output.

import numpy as np
from pprint import pprint

arr = np.random.randint(1, 10, size=(3, 3, 3))
print("Matrix:\n")
pprint(arr)

arr_sum = np.sum(arr, axis=1)
print("\nMatrix sum along axis 1:\n")
pprint(arr_sum)

Summation along axis 2

Matrix sum along axis 2 in NumPy gives us the row-wise sum of the matrix.

import numpy as np
from pprint import pprint

arr = np.random.randint(1, 10, size=(3, 3, 3))
print("Matrix:\n")
pprint(arr)

arr_sum = np.sum(arr, axis=2)
print("\nMatrix sum along axis 2:\n")
pprint(arr_sum)

Adding two NxNxN 3D matrices

We can perform element-wise addition of two matrices using np.add() function.

import numpy as np
from pprint import pprint

arr1 = np.random.randint(1, 10, size=(2, 2, 2))
print("Matrix 1:\n")
pprint(arr1)

arr2 = np.random.randint(1, 10, size=(2, 2, 2))
print("\nMatrix 2:\n")
pprint(arr2)

summ = np.add(arr1, arr2)
print("\nMatrix Addition:\n")
pprint(summ)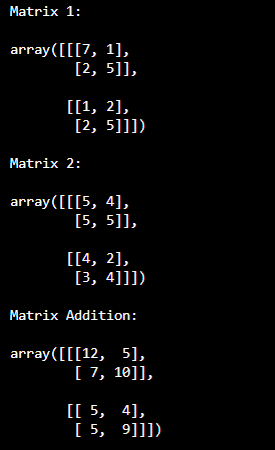

Similarily, we can perform elementwise subtraction, multiplication and division using np.subtract(), np.multiply() and np.divide() functions.

Matrix Multiplication of 3D NxNxN matrix in Python 3 with NumPy

Matrix multiplication of two compatible matrices can be done using the matmul function of NumPy.

import numpy as np
from pprint import pprint

arr1 = np.random.randint(1, 10, size=(2, 2, 2))
print("Matrix 1:\n")
pprint(arr1)

arr2 = np.random.randint(1, 10, size=(2, 2, 2))
print("\nMatrix 2:\n")
pprint(arr2)

summ = np.matmul(arr1, arr2)
print("\nMatrix Multiplication:\n")
pprint(summ)

NxNxN Matrix Multiplication in Python 3 with NumPy

Best 100+ Python Projects with source code

Also Read: