Euler’s Number in Python

   January 2, 2023
Euler's Number in Python

Today, we will throw light on Euler’s Number in Python. You must have used constants while dealing with Mathematics, Chemistry, Physics, etc. Constant in terms of mathematics means a well-defined object whose value cannot be changed. Constant play a very important role in Mathematics and Science as a part of the equation and balances out the phenomenon. Euler’s Numer is one of those famous constants in Mathematics.

The concept of exponentiation is nothing new, and it is related to logarithms. Logarithms have a base of 10 or e, where 10 is the most common base and e is Euler’s number.

What is Euler’s Number?

Euler’s number is a constant. That means, it is a fixed non-changeable value. It represents the basis of exponential functions and logarithms. Euler’s number is calculated and determined as the maximum growth after continuous compounding at a 100% growth rate.

Mathematically, Euler’s number is defined as:

Euler's Number in mathematics

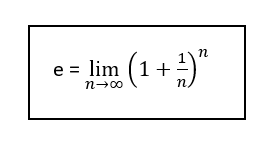
Where ‘e’ here represents Euler’s number or Eulerian Number or Napier’s constant.
And the value of e is 2.71828……

It is a continuous never-ending irrational number that is useful in dealing with exponentials, calculus, trigonometry, and differential equations.

Euler’s Number in Python

Python supports such constant values as its user needs in calculation operations. The advantage is, users don’t have to specify or define their values explicitly. They can just import the math library and use the constants with the corresponding call.

Python math module supports inbuilt functions for mathematical tasks. It supports the user to deal with trigonometry, powers, exponentials, factorials, and calculus, i.e. all the basic mathematical needs. This math module also defines some constants used in everyday mathematical tasks. There are 5 mathematical constants the library supports, they are:

  1. math.e: returns Euler’s number = 2.7182…
  2. math.inf: returns a floating point positive infinity value
  3. math.nan: returns a floating point Not a Number value
  4. math.pi: returns the value of pi = 3.1415…
  5. math.tau: returns the value of tau = 6.2831…

How to use Euler’s Number in Python?

1. Using math.e

Import the math module and call the class variable

#import module
import math

Euler = math.e
print("Euler's number is: ",Euler)

Output:

Euler's number is:  2.718281828459045

2. Using math.exp()

import math

Euler = math.exp(1)
print("Euler's number is: ",Euler)

Output:

Euler's number is:  2.718281828459045

If we compare both ways, it is almost the same.

import math
Euler1 = pow(math.e,2)
Euler2 = math.exp(2)

print(f"Euler1: {Euler1}, Euler2: {Euler2}")

Output:

Euler1: 7.3890560989306495, Euler2: 7.38905609893065

Examples of Euler’s Number in Python

Example 1:

Let’s evaluate some expressions containing e with Python’s eval(). eval() evaluates the argument expression. However, it should be a valid mathematical expression, otherwise, the function will throw an error.

import math

exp1 = eval("2+4*math.e")
exp2 = eval("2+4*math.exp(1)")
exp3 = eval("-math.e + 1")

print(exp1,exp2,exp3,sep="\n")

Output:

12.87312731383618
12.87312731383618
-1.718281828459045

The exp3 denotes adding a positive one to negative e.

Example 2:

The important use of e is in natural logarithms.

Let’s design a function that takes user input a number and returns the log of that number is base 10 and e.

def evaluate(n):
    log1 = math.log(n,10)
    log2 = math.log(n,math.e)
    return [log1,log2]
    
n=int(input("Enter a number: "))
print(f"Log with base 10: {evaluate(n)[0]}", f"Log with base e: {evaluate(n)[1]}", sep="\n")

Output:

Enter a number: 4
Log with base 10: 0.6020599913279623
Log with base e: 1.3862943611198906

We can really see a difference between the values, and the function returns.

Example 3:

The Euler’s constant is the maximum growth at continuous compounding. Let’s showcase this fact.

Remember the formula we discussed earlier for Euler’s number? Let’s plot the graph for it and see the increasing and then steady nature of the e.

import math
import matplotlib.pyplot as plt
 
import numpy as np

toplot = np.array([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17])
toplot = pow((1+ (1/toplot)),toplot)

plt.plot(toplot,color='green')
plt.xlabel("values")
plt.ylabel("exps")

Output:

euler's number graph

Example 4:

Let’s calculate Euler’s Number with factorial.

One of the formulas from Euler’s Number can be derived as,

e = 1 + 1/1! + 1/2! + 1/3! + 1/4! +…………+1/n!

Code:

e=0
for i in range(16):
    d = 1
    for j in range(1,i+1):
        d = d*j
    e = e +1/d
print("Euler's Number: ", e)

Output:

Euler's Number:  2.718281828458995

Example 5:

Let’s plot the powers of e

import math
import matplotlib.pyplot as plt
 
import numpy as np

toplot = np.exp(np.array([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]))

plt.plot(toplot,color='green')
plt.xlabel("values")
plt.ylabel("exps")

plt.show()

Output:

graph for powers of e

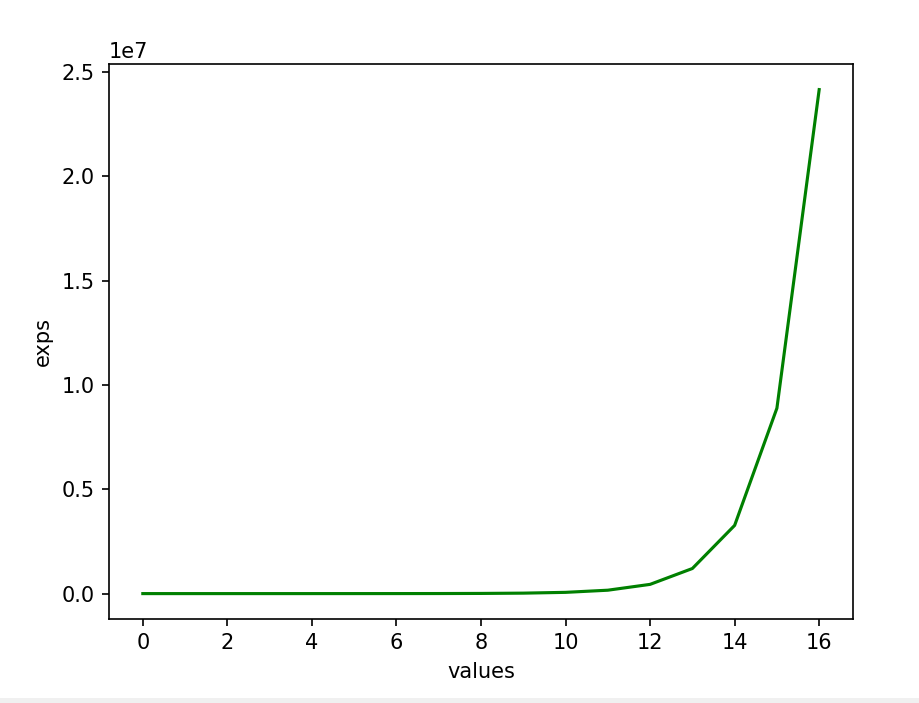
It is seen from the graph that the end curve is kind of constant.

Example 6:

Let’s plot y=e**x

import math
import matplotlib.pyplot as plt
 
import numpy as np

toplot = np.array([1,2,3,4,5,6,7,8,9,10])

toplot = pow(math.e,toplot)

plt.plot(toplot,color='green')
plt.xlabel("values")
plt.ylabel("exps")

plt.show()

Output:

graph for e ** x

Example 7:

Compound interest is an exponential growth, expressed as:

FV = PVert

where,
FV = Future value of balance or sum
PV = Present value of balance or sum
e = Euler’s constant
r = Interest being compounded
t = Time in years

Let’s design a program for this.

import math
def calculate(PV, r, t):
    e = math.e
    r = r/100
    i = r*t
    FV = PV * pow(e,i)
    
    return FV
   
PV = int(input("Enter Present Value of balance or sum: "))
r = int(input("Enter Rate of Interest: "))
t = int(input("Enter Time Period in Years: "))

FV = calculate(PV, r, t)
print(f"The sum {PV} with {r}% interest after {t} years will give: {FV}")

Output:

Enter Present Value of balance or sum: 1000
Enter Rate of Interest: 2
Enter Time Period in Years: 3
The sum 1000 with 2% interest after 3 years will give: 1061.8365465453596

These were some of the implementations of Euler’s Number in Python.

Euler’s number is one of the essential constants in Mathematics and calculates exponential growth or decay and finds its application in Physics, Calculus, Trigonometry, etc. Python supports this constant so you don’t need to define its value in the program.

Note: Euler’s Number and Euler’s Constant are two different concepts.

Thank you for visiting our website.

Best 100+ Python Projects with source code

Also Read:

Share:

Author: Ayush Purawr