Python Derivative Calculator

   July 13, 2022
Python Derivative Calculator

Introduction

Today, in this article, we will develop a Python Derivative Calculator, one of the most significant requirements of mathematics and statistics students all the time. Derivatives are also used for solving machine learning optimization problems. In order to move closer and closer to the maximum or minimum of a function, optimization methods such as gradient descent employ derivatives to determine whether to raise or reduce the weights.

The Derivative Calculator is an online tool for calculating the derivatives of functions.

What is Derivative?

A derivative is a function that quantifies slope. It is obtained by differentiating a function of the type y = f(x). When x is replaced with the derivative, the slope of the initial function y = f(x) is obtained.

There are several methods to describe the act of differentiation, often known as locating or calculating the derivative. The choice of notation is influenced by the kind of evaluated function and individual taste.

Suppose you have a generic function: y = f (x). The following notations may all be interpreted as “the derivative of y with respect to x” or, less technically, “the derivative of the function“

Now, Let’s take an example to understand this in detail :

Suppose we have the function: y= 5*x^3 +2*x^2+3*x+4

After applying all the rules of differentiation, we got the following result:

dy/dx=15*x^2+4*x+3

Logic Behind Derivative Calculator

Firstly, determine which portion of the original function (y = 5*x^3 +2*x^2+3*x+4) is of interest. For instance, imagine you need to determine the slope of y when the value of the variable x is 3. Substitute x = 3 into the slope function and solve:

dy/dx=15(3)^2+4*3+3=150

therefore, we found that when x=3, the function y has a slope of +150.

Code for Python Derivative Calculator

Now, how do we develop a derivative calculator? it’s a multi-step process. Let’s try to understand how we develop a derivative calculator in python.

Symbolic differentiation manipulates a given equation according to a variety of principles to create the equation’s derivative. Python can do symbolic differentiation if you know the equation whose derivative you want to calculate and for developing a Derivative Calculator we are using a SymPy(symbolic computation) python library.

Step1:

import the SymPy Library

For symbolic differentiation, we will need the SymPy package. y for symbolic mathematics in python there is a library called SymPy python library. It intends to be a comprehensive computer algebra system (CAS) that can be used as either a standalone application or a library for other applications. if SymPy is not installed in your python, kindly use the term:

pip install sympy

Other Python distributions, such as Anaconda, Enthought Canopy, etc., may already have SymPy. To validate, enter the following at the Python prompt:

from sympy import *

or

import sympy

Syntax:

from sympy import *

python SymPy library is really helpful in developing a standard derivative calculator or in performing other mathematical functions.

Step 2:

Make a Symbol:

In SymPy python, library variables are not automatically defined. you need to define them on your own or explicitly by using symbols. symbols produce Symbols from a string of variable names separated by space or commas. Symbol is essentially the same as a variable in SymPy on developing a derivative calculator we are using a list for defining the multiple symbols. 

symbol = int(input("Enter Number of Symbols in the equation"))
print(symbol)
symbol_list=[]
for i in range(0, symbol):
    print("Enter",i+1," symbol name" )
    item = (input())
    symbol_list.append(symbols(item))
print("symbol list is ", symbol_list)

if the equation has only one variable, you can define it as:

x=symbols('x')

if the equation has multiple variables, you can define them as:

x,y=symbols('x y')

these symbols can be used to create symbolic expressions in python are:

x**2+y+2*x
x^2+y+2*x

Step 3:

Create symbolic representation

So, by using Symbol x that we just defined, let’s create a symbolic expression(function) in Python for example function f(x) = 4x2+5x+8:

function=4*x**2+5*x+8

Step 4:

Calculate the derivative

Now, we’ll calculate the function’s derivative. Use the diff function to calculate derivates. The first argument of the diff function is the function whose derivative is desired. The second parameter should be the variable with regard to which the derivative is being computed.

der=Derivative(function,symbol_list)
  print(der)
  #you can take n derivative by taking the additional/ optional third argument 
  diff(function, symbol_list[0],n)
  variable=input("calculate the derivative on the basis of which variable?")
  df=diff(function,variable)
  print(df)

Step 5:

Calculating values within the expression

So we can create symbolic functions and calculate their derivatives, but how do we apply them? We must be able to enter a value and get a solution from these equations. With the subs approach, we may replace values with symbolic equations. The subs method substitutes a provided value for each occurrence of a variable. subs return a new expression; it has no effect on the original expression. Here, we substitute 3 for x in the df formula and initialize it in d: 

print("Now to substitute the values into symbolic equations, kindly enter the value")
  substitute=int(input())
  d=df.subs(variable, substitute)
  print(d)

Complete code for Python Derivative Calculator

from sympy import *
symbol = int(input("Enter Number of Symbols in the equation"))
print(symbol)
symbol_list=[]
for i in range(0, symbol):
    print("Enter",i+1," symbol name" )
    item = (input())
    symbol_list.append(symbols(item))
print("symbol list is ", symbol_list)
def deriv(symbol_list):
  function=input("enter function")
  function
  der=Derivative(function,symbol_list)
  print(der)
  #you can take n derivative by taking the additional/ optional third argument 
  diff(function, symbol_list[0],n)
  variable=input("calculate the derivative on the basis of which variable?")
  df=diff(function,variable)
  print(df)
  #substitute values into expressions
  print("Now to substitute the values into symbolic equations, kindly enter the value")
  substitute=int(input())
  d=df.subs(variable, substitute)
  print(d)

deriv(symbol_list)

Output:

Output for Python Derivative Calculator
Output for Python Derivative Calculator
Output for Python Derivative Calculator

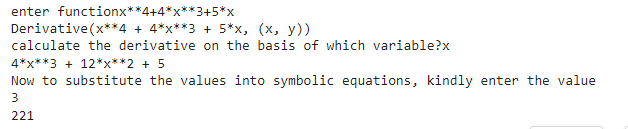
Conclusion

In this article, we see what is derivative and how can we create a Python Derivative Calculator. To create the derivative calculator using Python, we have used Python’s SymPy library in which Sym stands for the symbol. This was not tough but was not easy as well and we encourage you to research this topic and try more on this.

We hope you find this tutorial helpful.

Thank you for visiting our website.

Buy Python Handwritten Notes

Also Read:

Share:
Avatar of Ayush Purawr

Author: Ayush Purawr