Python Time Complexity Calculator

   July 21, 2022
Python Time Complexity Calculator

Introduction

In this article, we are going to develop a simple Project of Python Time Complexity Calculator. You can learn what is complexity and what is time complexity here. So, what is Time complexity? Time Complexity of an algorithm is calculated by counting the number of basic operations executed by the algorithm, assuming that each elementary operation takes a constant amount of time to execute.

Python Time Complexity Calculator

We will be using the big-o-calculator library for estimating the temporal or time complexity of sorting methods in Python. If the big-o-calculator is not installed in your python library, first of all, install it.

Installation

pip install big-o-calculator

You may evaluate time complexity, compute runtime, and compare two sorting algorithms with this big-o-calculator but sometimes results may vary.

Methods

There are a lot of methods available in the bio-o-calculator library, basically, it is a calculator to estimate the time complexity of a sorting function. Some of the important methods of bio-o-calculator library are test(), test_all(), runtime(), compare(),etc. All these methods contain many parameters. Now, let’s see Python Time Complexity Calculator code now.

Code

from bigO import BigO
from bigO import algorithm
from random import randint
fname=input("Enter algorithm name:")
def fname(array):  # in-place, unstable
    '''
    Best : O(n^2) Time | O(1) Space
    Average : O(n^2) Time | O(1) Space
    Worst : O(n^2) Time | O(1) Space
    '''
    currentIndex = 0
    while currentIndex < len(array) - 1:
        smallestIndex = currentIndex
        for i in range(currentIndex + 1, len(array)):
            if array[smallestIndex] > array[i]:
                smallestIdx = i
        array[currentIndex], array[smallestIndex] = array[smallestIndex], array[currentIndex]
        currentIndex += 1
    return array

def TimeComplexity(functionname):
    lib = BigO()
    cmplx = lib.test(functionname, "random")
    cmplx = lib.test(functionname, "sorted")
    cmplx = lib.test(functionname, "reversed")
    cmplx = lib.test(functionname, "partial")
    cmplx = lib.test(functionname, "Ksorted")

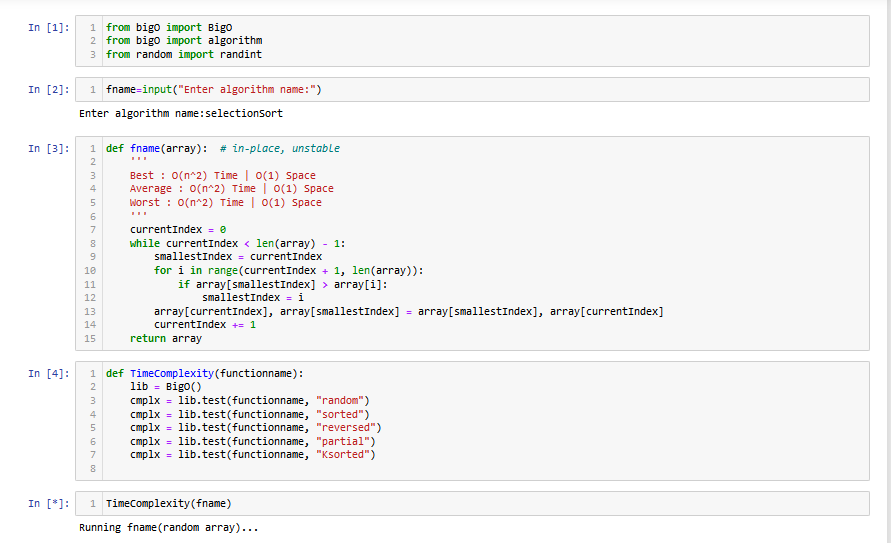
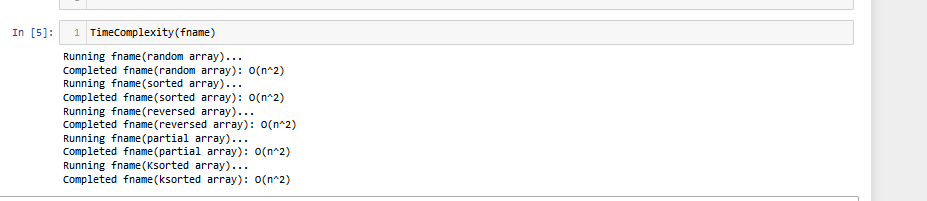
TimeComplexity(fname)

We are using the Selection Sort algorithm to understand the working of the big-o-calculator library of python.

python big o calculator
big o notation calculator python

Explanation:

For calculating the time complexity, you just need to enter the algorithm name and then define the function for this particular algorithm as we did with selectionSort in the example above. After that, we just test the algorithm with the help of the test() function of BigO and it will show all the results. You can test it with other algorithms as well.

Comparison of two algorithms

You can also compare two algorithms. For comparison, we need two algorithms. So, one we are taking bubble sort and second quick sort. Now, let’s see the Python Time Complexity Calculator code for a comparison of two algorithms.

Code

from bigO import BigO
from bigO import algorithm
from random import randint
fname=input("Enter algorithm name:")
fname1=input("Enter algorithm name")
def fname(array): #bubbleSort algorithm
    """
    Best:O(n) time| O(1) space
    Average: O(n^2) time | O(1) space
    Worst: O(n^2) time | O(1) space
    """
    n = len(array) 
    # Traverse through all array elements 
    for i in range(n): 
        # Last i elements are already in place 
        for j in range(0, n-i-1): 
            # traverse the array from 0 to n-i-1 
            # Swap if the element found is greater 
            # than check the next element 
            if array[j] > array[j+1]: 
                array[j], array[j+1] = array[j+1], array[j] 
def fname1(array):  # in-place | not-stable quicksort algorithm
    """
    Best : O(nlogn) Time | O(logn) Space
    Average : O(nlogn) Time | O(logn) Space
    Worst : O(n^2) Time | O(logn) Space
    """
    if len(array) <= 1:
        return array
    smaller, equal, larger = [], [], [] #taking 3 arrays small, equal and large
    pivot = array[randint(0, len(array) - 1)] #finding the pivot element
    for x in array:   #traverse each element of array
        if x < pivot:
            smaller.append(x) #if x element is smaller than pivot element then move it in small array 
        elif x == pivot:
            equal.append(x) #if x element is equal to pivot element then move it in equal array
        else:
            larger.append(x) # if x element is equal to pivot element then move it in large array
    return fname1(smaller) + equal + fname1(larger) #now again 
def TimeComplexity(functionname,functionname1):
    lib = BigO()
    cmplx = lib.test(functionname, "random")
    cmplx = lib.test(functionname, "sorted")
    cmplx = lib.test(functionname, "reversed")
    cmplx = lib.test(functionname1, "random")
    cmplx = lib.test(functionname1, "sorted")
    cmplx = lib.test(functionname1, "reversed")
    cmplx=lib.compare(fname,fname1,"random",5000)
    cmplx=lib.compare(fname,fname1,"all",5000)
  
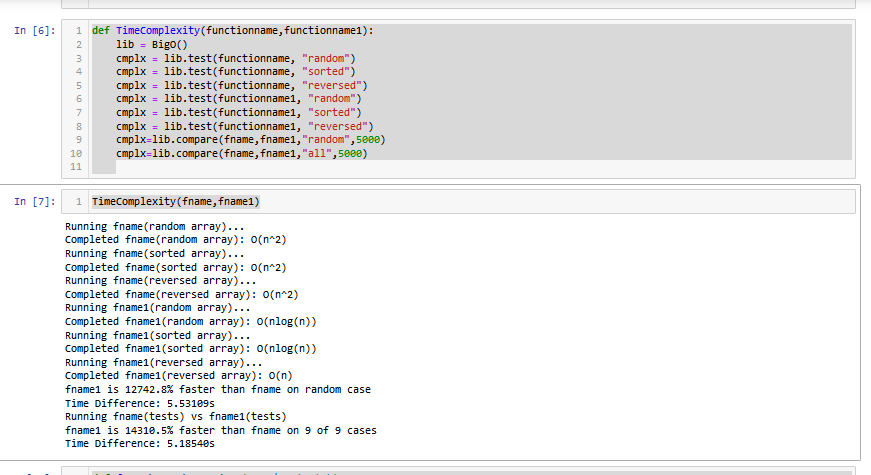
TimeComplexity(fname,fname1)

Explanation:

For comparing two algorithms we are using compare method of BigO.

  • fname is for bubbleSort algorithm and fname1 is for quickSort.
  • Select a random array with size 5000.
  • The second time we compare all types of arrays and the size is 5000 in all cases.
python time complexity calculator
big o calculator python
time complexity calculator python

Summary

Using the Python big-o-calculator library and some code, we have constructed a simple python time complexity calculator that allows us to simply compute the time complexity for different algorithms.

Thank you for reading this article, click here to start learning Python in 2022.

Buy Python Handwritten Notes

Also Read:

Share:

Author: Ayush Purawr