Until now we already have a pretty good grasp of how things work when it comes to regression and classification. Today let’s take a ride back and learn about one of the first ML algorithms i.e. KNN or K Nearest Neighbours. The idea behind the algorithm is pretty straightforward. But it’s not something to be underestimated but something to look forward to. In the end, I also have an interesting use case of KNN. Let’s see if you can guess what it is. If you haven’t already, check out the pandas tutorial on our website.
K Nearest Neighbours Intuition
As I said KNN is a very straightforward algorithm. It’s actually the only algorithm that has O(1) train complexity and no training process. What! That doesn’t make sense though if it doesn’t train how does it know what to predict? That’s an absolutely valid question after all from all we have studied we train our model w.r.t. our dataset. If we don’t train them how can we derive proper inference? The answer lies in the technique that KNN uses to predict the outcome. Yes, it has no training process but that means it has a longer predicting process too. Let’s understand it with an example.
Example of KNN Algorithm
Let’s say we have a friend named Garry who wants to buy a house in a colony. The thing is Garry has a habit of agreeing to the initial price no matter how high and the broker knows this and tries to take advantage of the situation. You came to know about this and asked Garry to let you do the bidding instead. The thing you noticed is that the whole area has a pattern i.e. the houses near each other have similar prices. Knowing this you came up with a way to place to bid the correct price.
You three searched for a while and by the end of the day, Garry found the house he liked a lot. The Broker told the price to settle for and being greedy he said a price of $50k which was quite far-fetched. You denied the claims of the house being so pricey, Broker looked angry and asked how much do you think it is. You knew the price of 3 nearby houses i.e. $20k, $30k, and $25k. So you offered the average price of those i.e. 25k. The broker looked shocked and apologized for tricking Garry. Garry thanked you and treated you to a nice restaurant for the help.
Working of K Nearest Neighbours
The above example is pretty similar to the working of KNN. What KNN does is that it finds the points in the training set near to the point you want to predict the target for and gives you the majority class or average values of targets of those points depending on the type of problem you are solving i.e. Classification or Regression. But where does the k comes into play? More importantly what it is?
Previously I said KNN finds points nearby to the one we want to predict but how many points do we find the majority or average for? k is the no. of nearest points to consider for inference. For example, if k = 5 that means that we’ll take the nearest 5 points to infer the values from. The name makes sense since it takes k nearest points into consideration to infer the value.
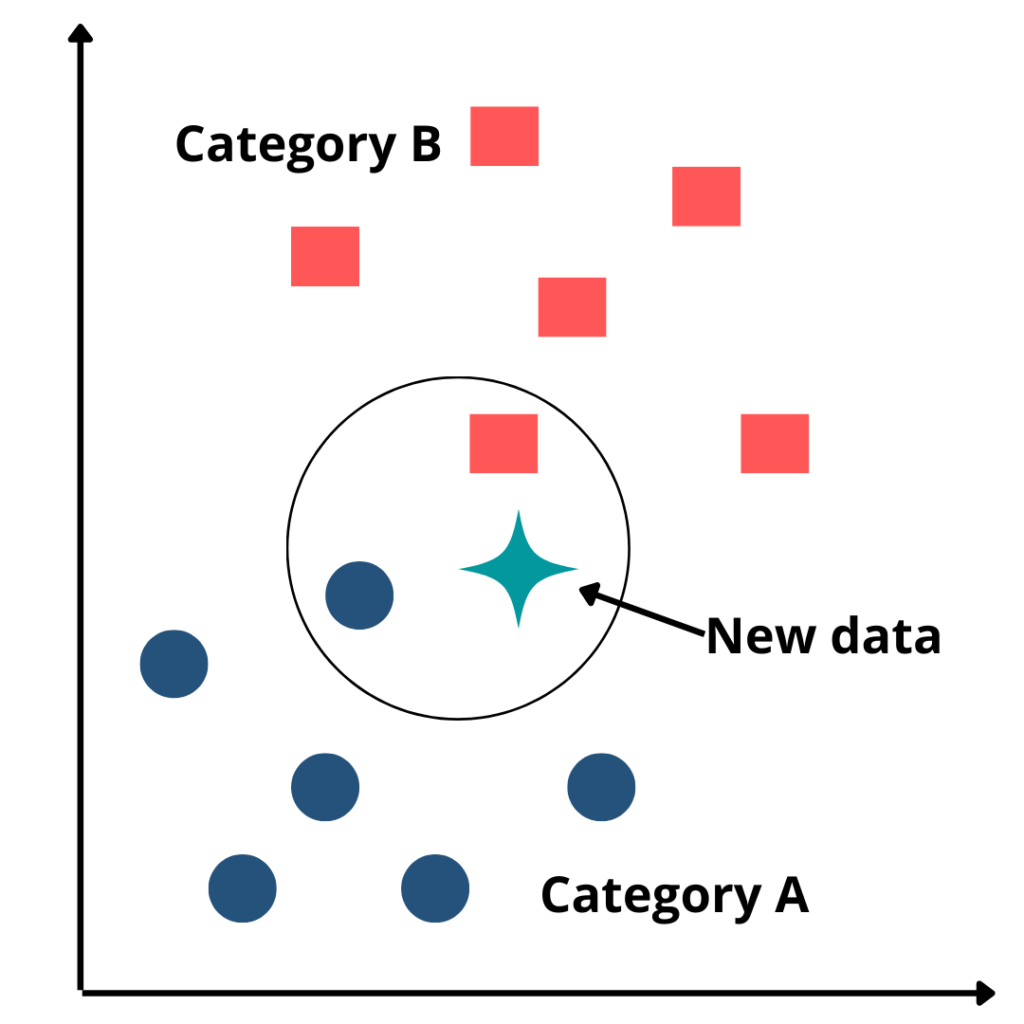
So how does this k affect the inference? The lower the value of k the more it is prone to overfit. The higher the value of k the more it is prone to be affected by outliers. Thus it is important to find the optimal value of k. Let’s see how we can do that.
Steps to build the K-NN algorithm
The K-NN working can be built on the basis of the below algorithm
Step-1: Select the number K of the neighbors. There is no particular way to determine the best value for “K”, so we need to try some values to find the best out of them. The most preferred value for K is 5. A very low value for K such as K=1 or K=2, can be noisy and lead to the effects of outliers in the model. Large values for K are good, but it may find some difficulties.
Step-2: Next, Calculate the Euclidean distance between the data points. The Euclidean distance is the distance between two points, which we have already studied in geometry.
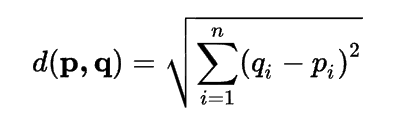
Step-3: Take the K nearest neighbors as per the calculated Euclidean distance. Some ways to find optimal k value are
- Square Root Method: Take k as the square root of no. of training points. k is usually taken as odd no. so if it comes even using this, make it odd by +/- 1.
- Hyperparameter Tuning: Applying hyperparameter tuning to find the best value of k.
- Schwarz Criterion: The fanciest and over-the-top thing you can do. This works by minimizing distortion + λDklogN. Let’s not talk about it ever again!
Step-4: Among these k neighbors, count the number of the data points in each category. KNN assumes that similar points are closer to each other.
Step-5: After that, let’s assign the new data points to that category for which the number of the neighbor is maximum. It groups to the category which is near the data point.
Step-6: And that’s it, our KNN model is ready.
Implementation of KNN using sklearn
This was the surprise I was talking about and congrats if you guessed it correctly. For previous tutorials, the walkthroughs were getting a bit monotonous so I thought to spice things up a bit. So let’s get started with this tutorial we’ll recognize faces in the dataset Olivetti faces present in sklearn’s dataset. Let’s start with importing the required libraries and then importing our data.
#Importing the required libraries import numpy as np from sklearn.datasets import fetch_olivetti_faces from sklearn.metrics import accuracy_score #Importing the data data = fetch_olivetti_faces() X = data.data Y = data.target
Now that we have our data let’s split it but one thing we see is that there are 40 different faces with 10 images of each face so when we split we want all the images in both sets. One way to make sure of that is to use stratify parameter which ensures the ratio of target classes is the same in the splits.
#Splitting the data into train and test data from sklearn.model_selection import train_test_split X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify = Y)
Let’s train our model
#Import knearest neighbors Classifier model from sklearn.neighbors import KNeighborsClassifier #Training the model clf = KNeighborsClassifier(n_neighbors=3) #Train the model using the training sets clf.fit(X_train, Y_train) #Predict the response for test dataset Y_pred = clf.predict(X_test)
Let’s find the accuracy which in this case came out to be 0.86.
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Calculating the Model Accuracy
print("Accuracy:",metrics.accuracy_score(Y_test, Y_pred))Yay! You created a face recognition model with such ease and celebration. Also, KNN is pretty well suited for it given same faces are bound to have similar points making them cluster together near each other.
Advantages of K Nearest Neighbours
- No Training Period: It does not learn anything in the training period. It does not derive any discriminative function from the training data.
- Data can be updated easily and will not impact the accuracy of the algorithm.
- KNN algorithm is easy to implement
Disadvantages of K Nearest Neighbours
- Normalizing data is important else it could potentially lead to bad predictions.
- This algorithm doesn’t work well with large datasets.
- It doesn’t work well with high-dimension datasets.
Conclusion
Hope you have enjoyed this article about the KNN algorithm. We have looked into the KNN algorithm and its implementation in this article. Will meet you in the next article with an exciting new topic!
Credits: Edureka!
Also Read:
- Flower classification using CNNYou know how machine learning is developing and emerging daily to provide efficient and hurdle-free solutions to day-to-day problems. It covers all possible solutions, from building recommendation systems to predicting something. In this article, we are discussing one such machine-learning classification application i.e. Flower classification using CNN. We all come across a number of flowers…
- Music Recommendation System in Machine LearningIn this article, we are discussing a music recommendation system using machine learning techniques briefly. Introduction You love listening to music right? Imagine hearing your favorite song on any online music platform let’s say Spotify. Suppose that the song’s finished, what now? Yes, the next song gets played automatically. Have you ever imagined, how so?…
- Top 15 Python Libraries For Data Science in 2022
Introduction In this informative article, we look at the most important Python Libraries For Data Science and explain how their distinct features may help you develop your data science knowledge. Python has a rich data science library environment. It’s almost impossible to cover everything in a single article. As a consequence, we’ve compiled a list… - Top 15 Python Libraries For Machine Learning in 2022
Introduction In today’s digital environment, artificial intelligence (AI) and machine learning (ML) are getting more and more popular. Because of their growing popularity, machine learning technologies and algorithms should be mastered by IT workers. Specifically, Python machine learning libraries are what we are investigating today. We give individuals a head start on the new year… - Setup and Run Machine Learning in Visual Studio Code
In this article, we are going to discuss how we can really run our machine learning in Visual Studio Code. Generally, most machine learning projects are developed as ‘.ipynb’ in Jupyter notebook or Google Collaboratory. However, Visual Studio Code is powerful among programming code editors, and also possesses the facility to run ML or Data… - Diabetes prediction using Machine Learning
In this article, we are going to build a project on Diabetes Prediction using Machine Learning. Machine Learning is very useful in the medical field to detect many diseases in their early stage. Diabetes prediction is one such Machine Learning model which helps to detect diabetes in humans. Also, we will see how to Deploy… - 15 Deep Learning Projects for Final year
Introduction In this tutorial, we are going to learn about Deep Learning Projects for Final year students. It contains all the beginner, intermediate and advanced level project ideas as well as an understanding of what is deep learning and the applications of deep learning. What is Deep Learning? Deep learning is basically the subset of… - Machine Learning Scenario-Based QuestionsHere, we will be talking about some popular Data Science and Machine Learning Scenario-Based Questions that must be covered while preparing for the interview. We have tried to select the best scenario-based machine learning interview questions which should help our readers in the best ways. Let’s start, Question 1: Assume that you have to achieve…
- Customer Behaviour Analysis – Machine Learning and Python
Introduction A company runs successfully due to its customers. Understanding the need of customers and fulfilling them through the products is the aim of the company. Most successful businesses achieved the heights by knowing the need of customers and dynamically changing their strategies and development process. Customer Behaviour Analysis is as important as a customer… - NxNxN Matrix in Python 3
A 3d matrix(NxNxN) can be created in Python using lists or NumPy. Numpy provides us with an easier and more efficient way of creating and handling 3d matrices. We will look at the different operations we can provide on a 3d matrix i.e. NxNxN Matrix in Python 3 using NumPy. Create an NxNxN Matrix in… - 3 V’s of Big dataIn this article, we will explore the 3 V’s of Big data. Big data is one of the most trending topics in the last two decades. It is due to the massive amount of data that has been produced as well as consumed by everyone across the globe. Major evolution in the internet during the…
- Naive Bayes in Machine Learning
In the Machine Learning series, following a bunch of articles, in this article, we are going to learn about the Naive Bayes Algorithm in detail. This algorithm is simple as well as efficient in most cases. Before starting with the algorithm get a quick overview of other machine learning algorithms. What is Naive Bayes? Naive Bayes… - Automate Data Mining With PythonIntroduction Data mining is one of the most crucial steps in Data Science. To drive meaningful insights from data to take business decisions, it is very important to mine the data. Deleting or ignoring unnecessary and unavailable parts of data and focusing on the correct and right data is beneficial, and more if required in…
- Support Vector Machine(SVM) in Machine Learning
Introduction to Support vector machine In the Machine Learning series, following a bunch of articles, in this article, we are going to learn about Support Vector Machine Algorithm in detail. In most of the tasks machine learning models handle like classifying images, handling large amounts of data, and predicting future values based on current values,… - Convert ipynb to Python
This article is all about learning how to Convert ipynb to Python. There is no doubt that Python is the most widely used and acceptable language and the number of different ways one can code in Python is uncountable. One of the most preferred ways is by coding in Jupyter Notebooks. This allows a user… - Data Science Projects for Final Year
Do you plan to complete your data science course this year? If so, one of the criteria for receiving your degree can be a data analytics project. Picking the best Data Science Projects for Final Year might be difficult. Many of them have a high learning curve, which might not be the best option if… - Multiclass Classification in Machine Learning
Introduction The fact that you’re reading this article is evidence of the fact that you’ve finally realised that classification problems in real life are rarely limited to a binary choice of ‘yes’ and ‘no’, or ‘this’ and ‘that’. If the number of classes that the tuples can be classified into exceeds two, the classification is… - Movie Recommendation System: with Streamlit and Python-ML
Have you come across products on Amazon that is recommended to you or videos on YouTube or how Facebook or LinkedIn recommends new friend/connections? Of course, you must on daily basis. All of these recommendations are nothing but the Machine Learning algorithms forming a system, a recommendation system. Recommendation systems recommend relevant items or content… - Getting Started with Seaborn: Install, Import, and Usage
Seaborn Library in Python Seaborn is a visualization library for plotting good-looking and stylish graphs in Python. It provides different types of styles and color themes to make good-looking graphs. The latest version of the seaborn library is 0.11.2. Installation Mandatory dependencies numpy (>= 1.9.3) scipy (>= 0.14.0) matplotlib (>= 1.4.3) pandas (>= 0.15.2) Importing Seaborn Library Using Seaborn Library… - List of Machine Learning Algorithms
In this article on the list of Machine Learning Algorithms, we are going to learn the top 10 Machine Learning Algorithms that are commonly used and are beginner friendly. We all come across some of the machines in our day-to-day lives as Machine Learning is making our day-to-day life easy from self-driving cars to Amazon virtual assistant “Alexa”….
